Reasoning about Numbers
See also applets under the heading Fractions & Decimals
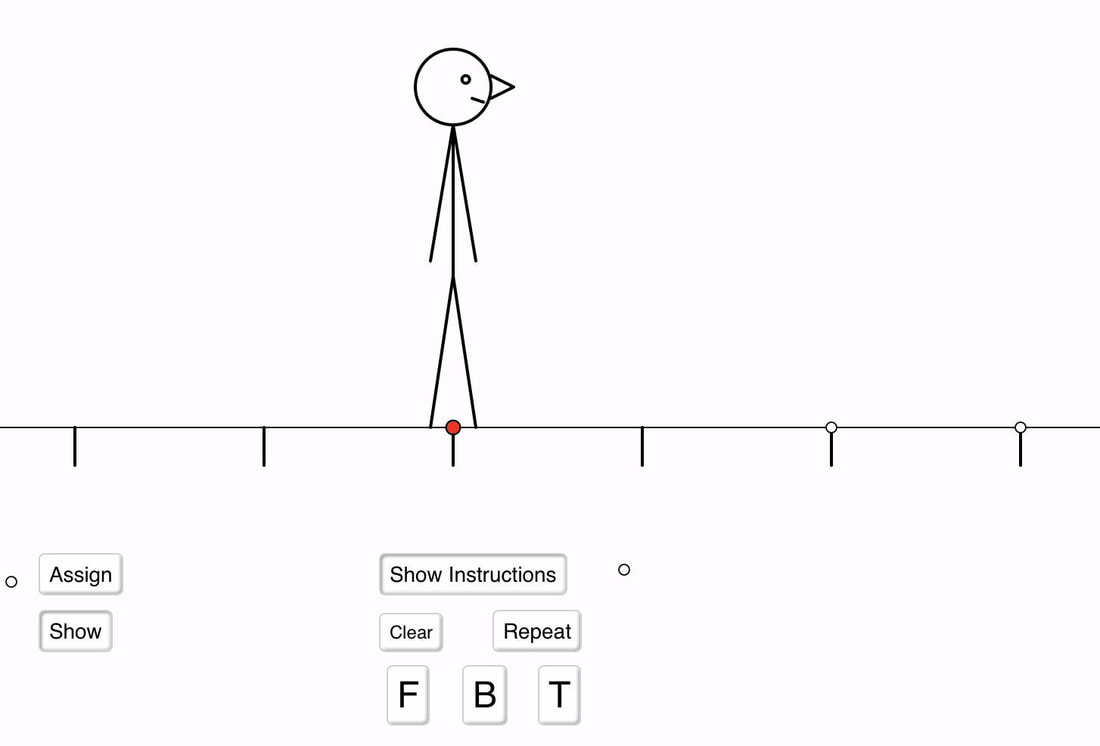
Number Line MovementsInitially this is a virtual version of walking forwards and backwards on a number line, in order to emphasise arithmetic as the study of actions of numbers on numbers.
With the addition of T (for turn around) learners can begin to reason about the actions without recourse to doing it physically, and eventually, without enacting it virtually. Download applet (with notes) |

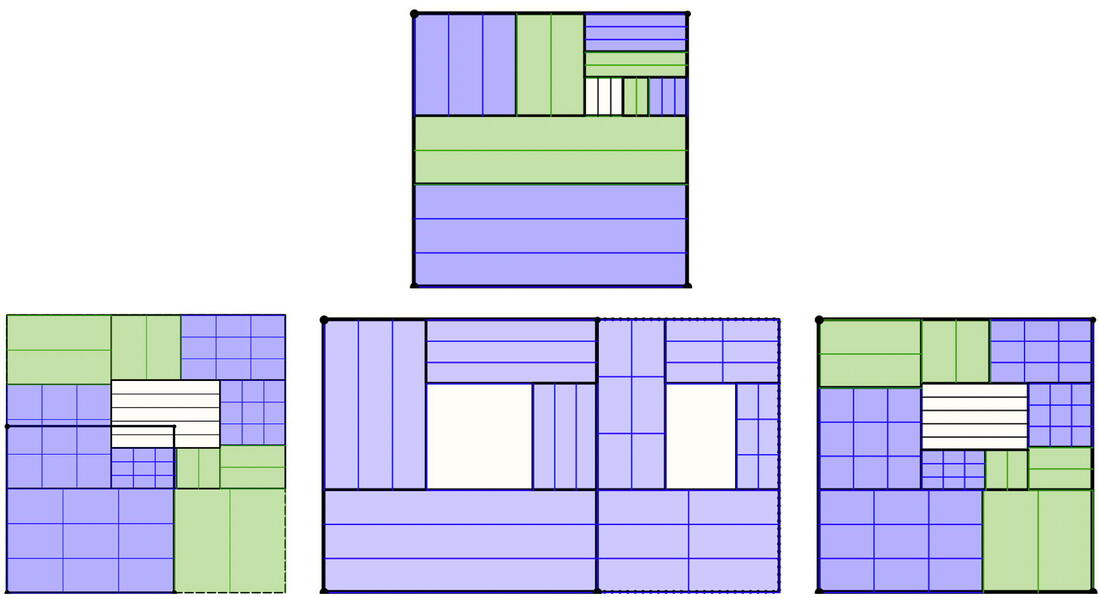
Multiplicative Reasoning: The Drakensberg Grids
APPLETS:
Notes on applet use are included in these zipped folders.
Drakensberg Grids: html & notes
Drakensberg Grids: html, notes & Source files
Going with the grain (down a column) provides variation of numbers.
Going across the grain (along a row) provides variation of presentation.
A second app in the folder presents a single row so that scaling is much larger.
|
Varied Multiplications
What is the same and what is different about these five calculations? Why? How might they be extended to the rest of the grid? The applet permits the numbers to be changed, and also reveals reasoning behind the phenomenon |
|
|
Sharing OutIf you have ever picked berries, or shared things out as a child, you may recognise "3 for me and 2 for the pot" or "3 for me and 2 for you"!
What sorts of mathematical questions can you ask about this sort of situation? In how many different ways can you express the relationships between the number of blue, green and total after the process has been going on for an unspecified length of time? The idea is to introduce or to work on relationships between the language of fractions and decimals, both seen as actions on a set of objects. The applet permits choices of from 2 to 5 colours, in integer ratios. |
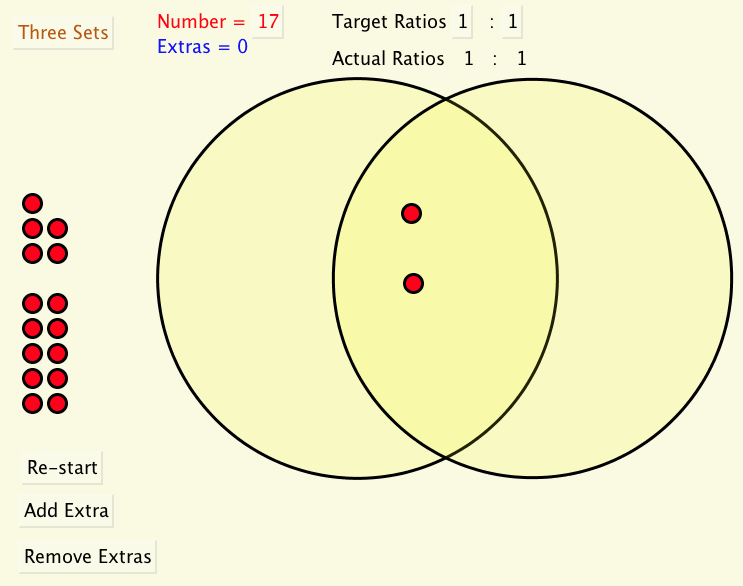
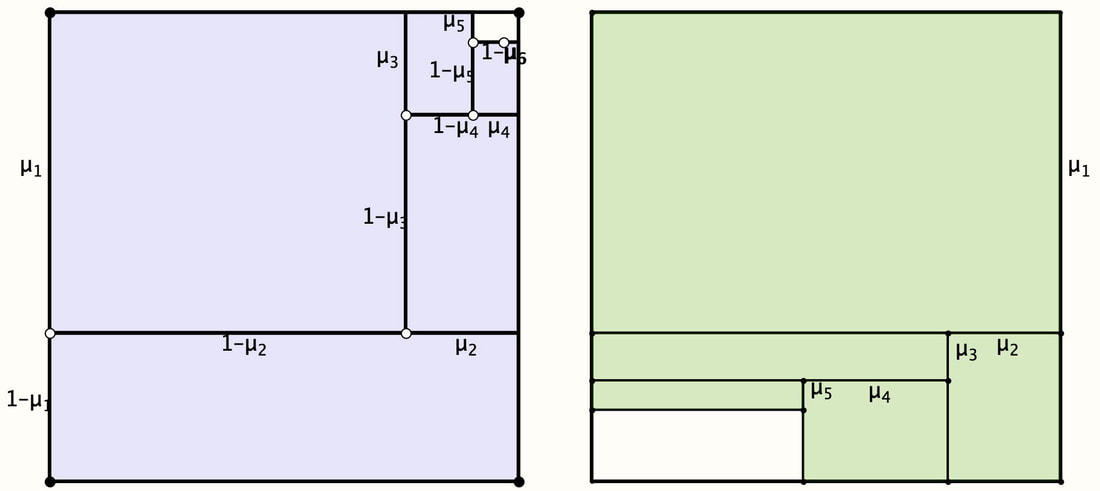
Set RatiosGiven a number of counters, in how many different ways can you place them in the three regions formed from two overlapping Circles (sets A and B) so that there are the same number of counters in both A and B?
What if the ratio is to be 3:2 for A:B? and more generally? What if there are three sets?
|
Screen shot | ||||||
|
Screen shot
|
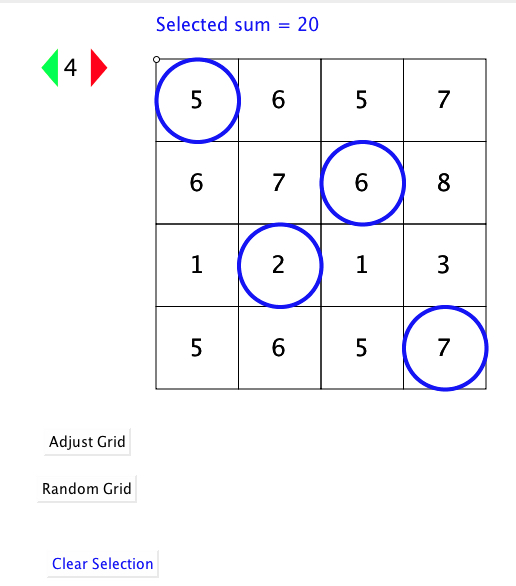
Covered-Up SumsA selection of cells from a grid have been selected (think of the other cells as having been covered-up). Their sum is shown.
Make another selection, one cell from each row and columns. What is their sum? What is going on? What happens if you cover-up all but two cells in each row and column? The applet supports constructing your own grid with a specified sum. What matters is the reasoning as to why, and why the construction works!
| ||||||
|
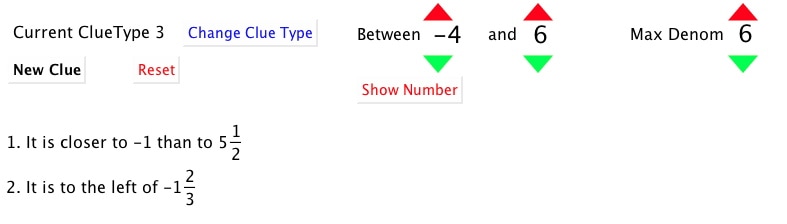
Reasoning About Order on the Number Line
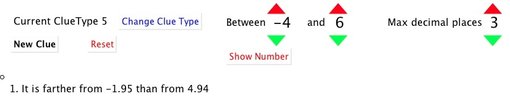
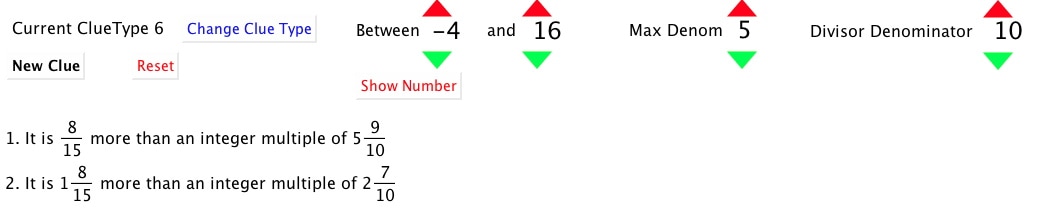
Using to the left of, to the right of, greater than and less, and also closer to ... than to ... to work out a number on the number line. One deals with whole numbers; one deals with fractions, and one deals with decimals. One uses clues of the form "the number is ... much more than an integer multiple of ..." where the divisors can be chosen to have denominators from 1 to 10. Still an early draft! Applets |
Screen shots from the various applets
Whole Number Searching
Decimal Searching
Fraction Searching
Remainder Reasoning
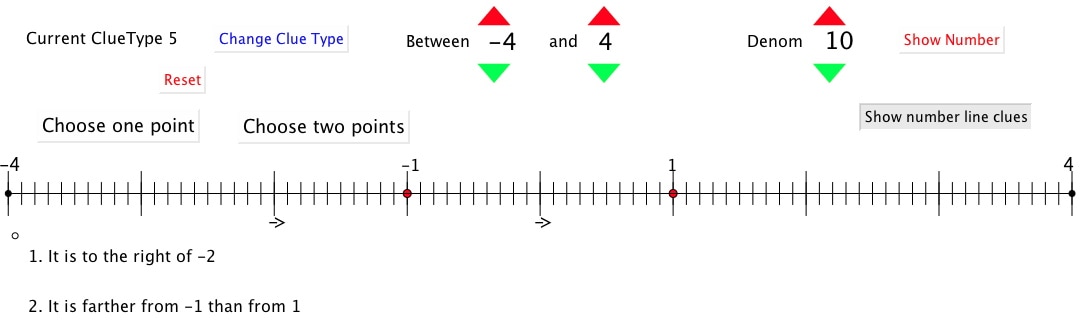
Number Line Reasoning
|
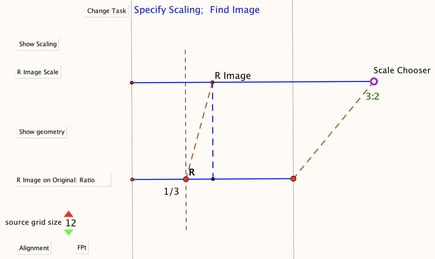
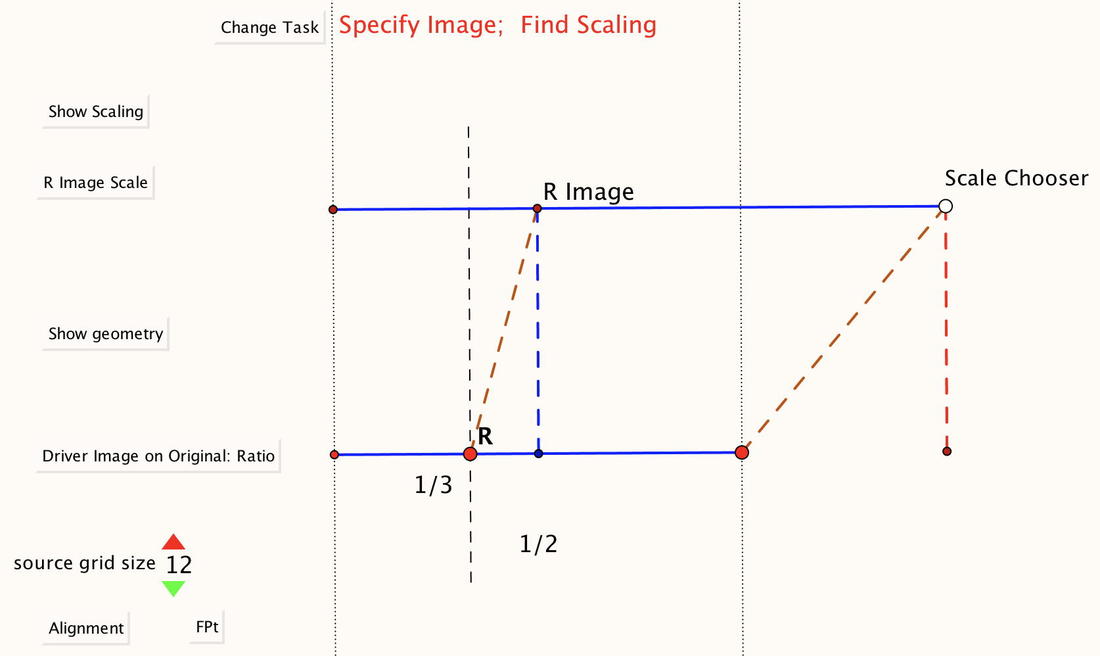
Elastic Multiplication
|
This applet is dedicated to the notion that multiplication in school is scaling, of which related addition is only one manifestation.
The applet presents an elastic which can be stretched and contracted, while maintaining a copy of the original with which to make comparisons. The fixed-point of the stretching can be at the left-hand end, or somewhere along the elastic. Two types of questions can be posed: 1) given a scale factor, where does an identified point on the original , when scaled, end up aligned with on the original? 2) given that an identified point on the original has needed up aligned on the original with some other point, what was the scale factor? By changing the fixed point, addition, subtraction, multiplication and division of fractions are involved. |
Altered Products
|
This is a Structured Variation grid based around some simple numerical facts about products of related numbers.
The picture shows part of the grid with some of the entries filled in, from which all the other entries can be predicted. Working with the grid, you fill in entries by clicking having predicted. The grid is available here: altered products |
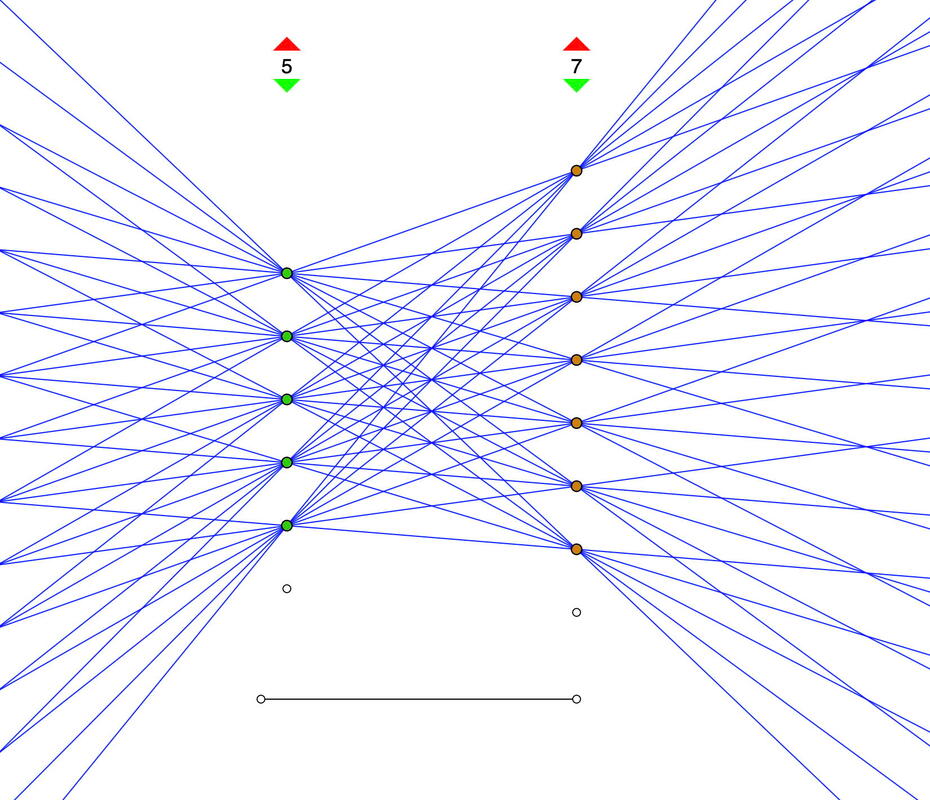
N-M Bipartite Correspondences Depicted
|
Freudenthal suggested that bipartite graphs are an important underlying awareness for a multiplicative sense of number.
This applet draws pictures like this one, which may raise a number of counting questions. At its heart is the awareness that to count the number of lines, so many dots are each connected to so many dots. download Applet |
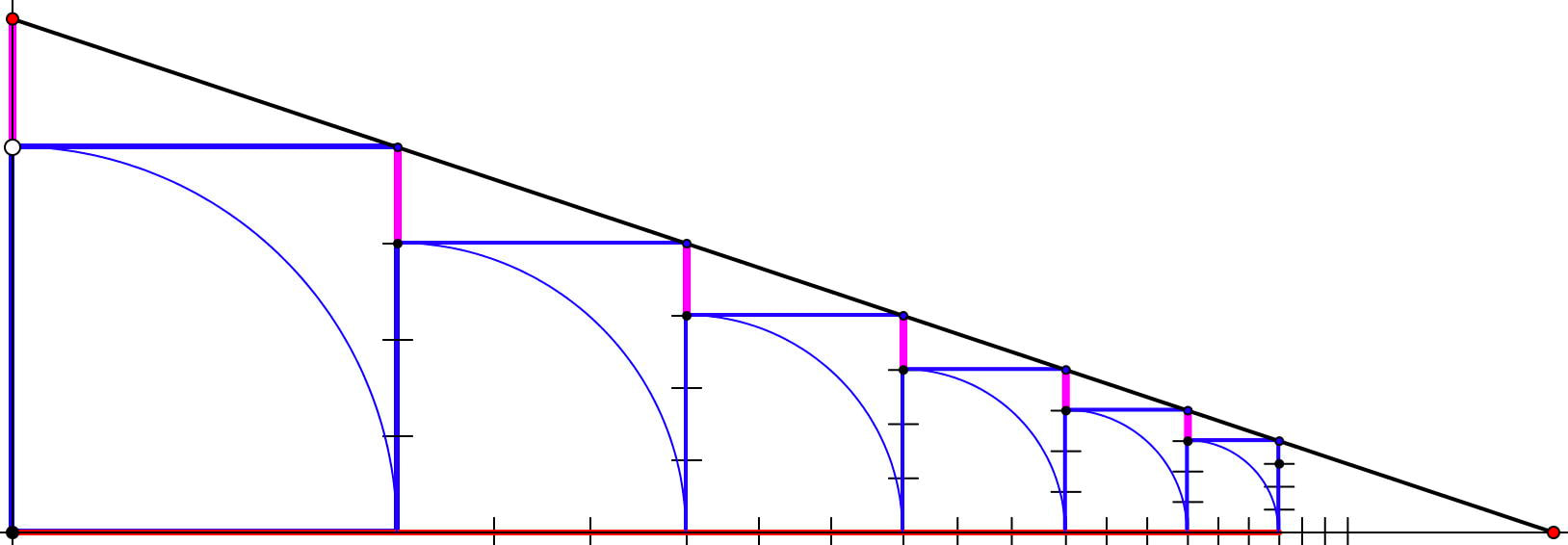
Summing Infinite Sequences: going beyond GPs
|
A suite of applets which enable exploration of different ways to display infinite Geometric Progressions, and then extending to other sequences in which the ratio varies.
GP Sums offers opportunities to 'read' diagram sequences so as to give the sum to n terms, and the infinite sum.
I usually start with a ratio of ½, then go to ratios less than ½ , before showing 4 different ways to sum when the ratio is greater than ½. The approach generalises to sequences for which the ratio varies in some systematic manner: one applet permits direct intervention term by term,; the other promotes a theoretical or general approach. An alternative display uses slopes of lines and will extend to series in which the ratio varies in some systematic manner. Applet Package including notes is still incomplete but will be updated in time. PPT using static images |