|
|
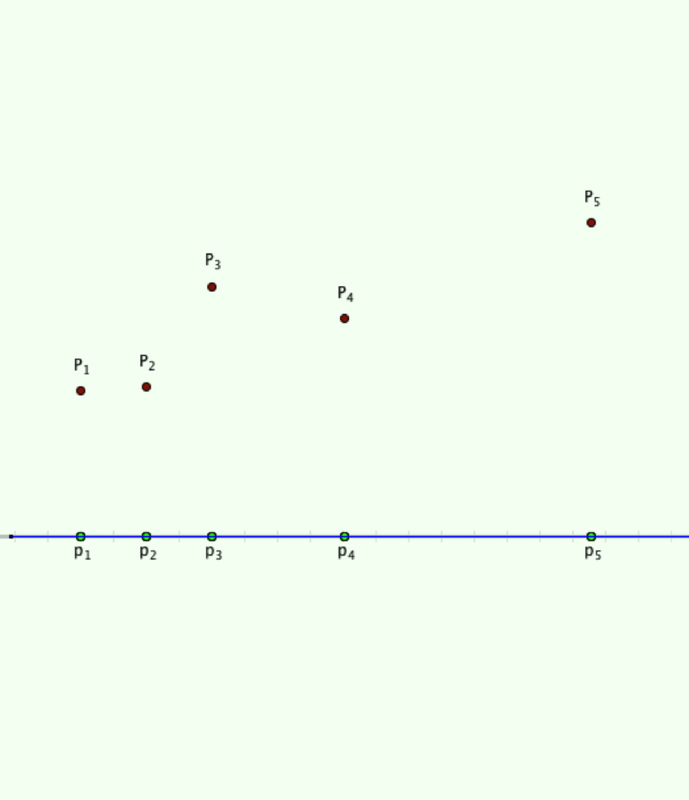
Predicting a Quartic
The five points determine a unique quartic polynomial. What might it look like? How does it change if just one of the points is moved up or down vertically? Clicking on the picture accesses an applet that provides up to 8 points together with buttons that introduce random extra points, a dynamic locus, and the actual graph. |
|
|
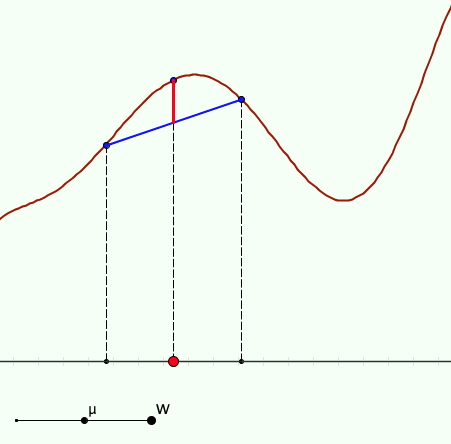
Chordal Gaps
The blue chord has a fixed width controlled by w. At the mid-point (more generally the mu point) the gap between chord and function is shown in red. The chordal gap can be plotted by animating the red point (X). What happens to the chordal gap as the chord width approaches 0? What happens to the chordal gap divided by the chord width? What happens to the chordal gap divided by the square of the chordal width? This and more can be explored in the applet (click on the image). |
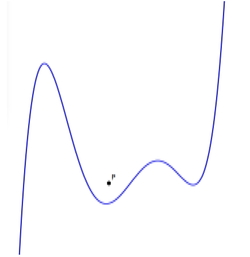
Tangent Power
The Tangent Power of a point P with respect to a function f is the number of tangents to f through P.
What determines the boundaries of the regions with the same tangent power?
Can you develop a method of determining these without simply doing lots of examples?
Pay attention to how you find the tangent power of a point ... there might be a better way!
Click on the picture to access an applet for exploring this idea.
The Tangent Power of a point P with respect to a function f is the number of tangents to f through P.
What determines the boundaries of the regions with the same tangent power?
Can you develop a method of determining these without simply doing lots of examples?
Pay attention to how you find the tangent power of a point ... there might be a better way!
Click on the picture to access an applet for exploring this idea.
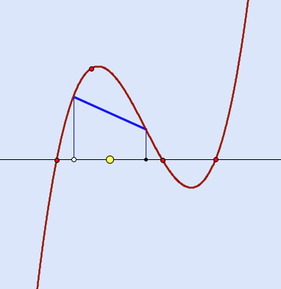
Cubic Chords
Here you see a cubic, the yellow point it the midpoint between two of its roots, and a chord with the same midpoint.
Where will the chord, when extended, meet the cubic?
What about the tangent corresponding to the yellow point?
What happens if the yellow point is moved but all chords have it s the associated midpoint?
Applet
These ideas can be generalised to higher degree polynomials.
See Mason, J. (2011). Mean-Invariant Polynomial Intersections: a case study in generalisation. Technology, Knowledge and Learning Journal 16 (2) p183-192. DOI: 10.1007/s10758-011-9185-y
Here you see a cubic, the yellow point it the midpoint between two of its roots, and a chord with the same midpoint.
Where will the chord, when extended, meet the cubic?
What about the tangent corresponding to the yellow point?
What happens if the yellow point is moved but all chords have it s the associated midpoint?
Applet
These ideas can be generalised to higher degree polynomials.
See Mason, J. (2011). Mean-Invariant Polynomial Intersections: a case study in generalisation. Technology, Knowledge and Learning Journal 16 (2) p183-192. DOI: 10.1007/s10758-011-9185-y
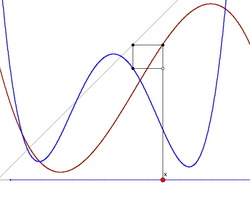
Cobwebs
The applet animates the red point X and the construction follows it.
The grey line is y = x.
What is the locus of the white point?
Other follow-up tasks emerge from using the applet.
Applet Notes
The applet animates the red point X and the construction follows it.
The grey line is y = x.
What is the locus of the white point?
Other follow-up tasks emerge from using the applet.
Applet Notes