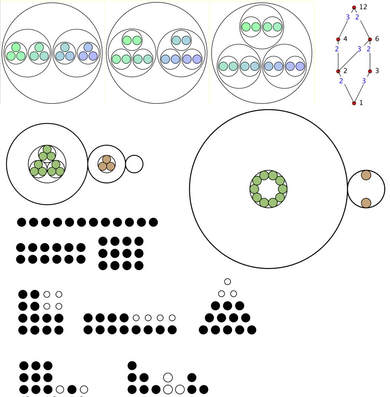
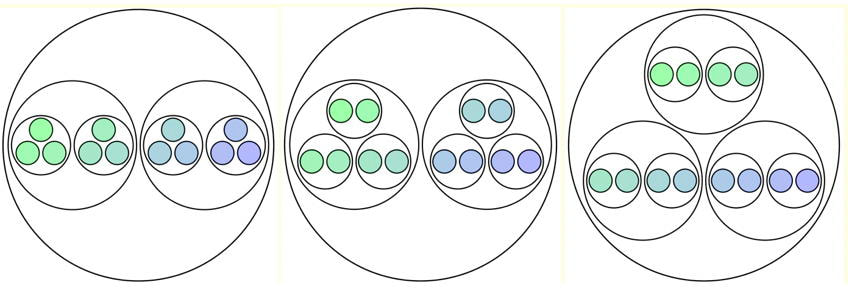
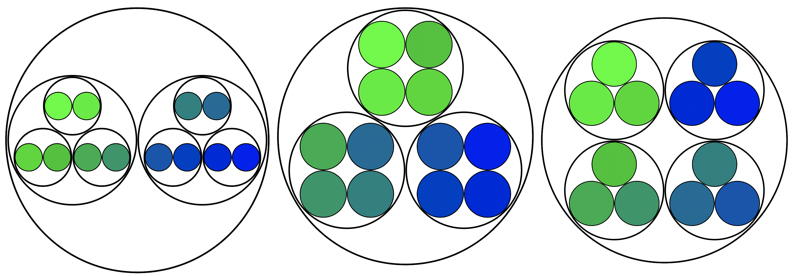
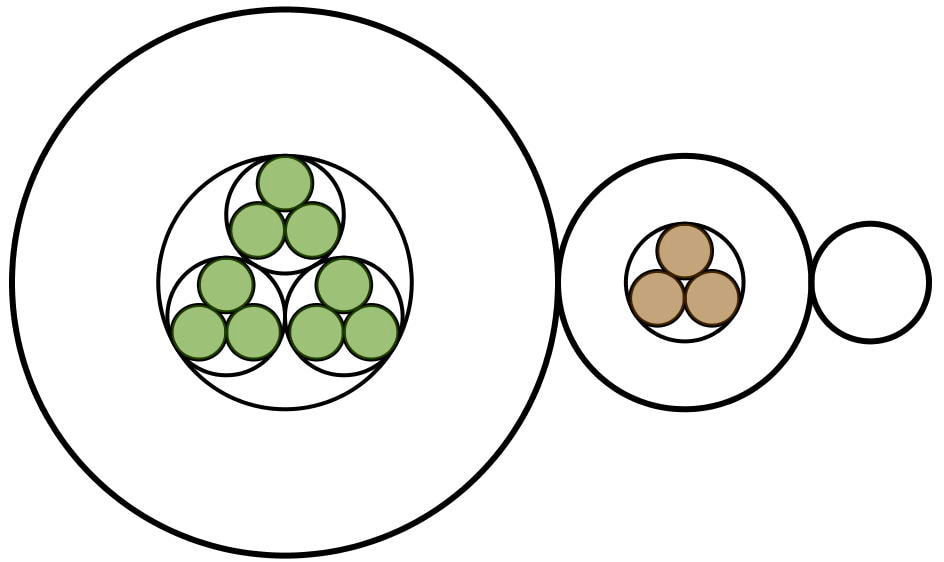
Numbers as "lots of" "lots of"...
|
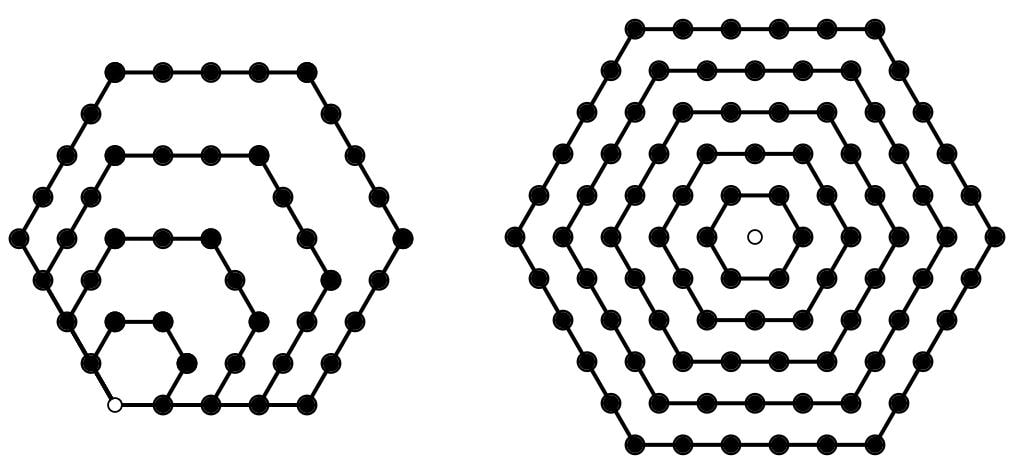
Inspired by Stephen Yorgey's 'necklace' numbers, and Stephen von Worley's animated sequence of these, I constructed an applet that gives individual control over the number being formatted and the order in which the primes are used. They may be useful for immersing learners in the multiplicative structure of numbers Notes are included with the applets. Applet: "Lots of" Numbers ( File has to be unzipped!) Numbers can be shown in sequence, or generated at random; Different orders of prime factors gives different diagrams. Also included are applets for counting in different bases, for displaying the GCD (HCF) and LCM of a pair of numbers, and for comparing the collection of all factor trees (as a single factor lattice) and paths within that lattice with the different ways of displaying "Lots of" for a given number. |
"Lots of" Diagrams for 12 (above) and using 4's when possible (below)
|
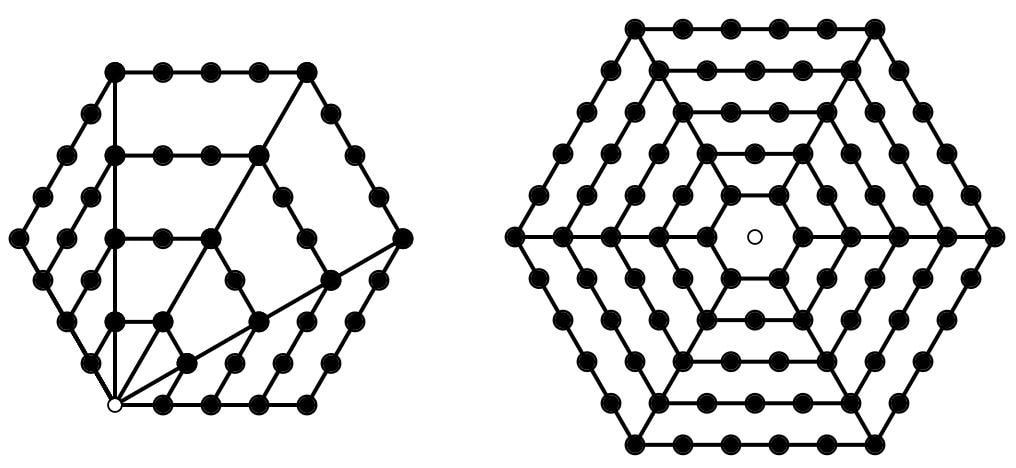
"Lots of" Displays for Different Bases
|
12 presented in base 3
|
The use of different bases arises quite naturally in the following form:
You have cards with symbols from some otherwise unknown language, showing 0, 1, 2 and 3. You have a collection of counters, and you need to inform someone who reads and understands only this other language, how many counters you have. The task is inspired by Zoltan Dienes, and refined by many people, including Tony Wing (UK) and Kieren Egan (Canada). Applet: Necklace Bases see applets in "Lots of" |
Numbers as arrays of counters
|
Numbers as Rectangular Arrays
Numbers as Differences of square numbers, differences of triangular numbers, differences of similar rectangular numbers Numbers as sums of at most 3 triangular numbers Numbers as sums off at most 4 square numbers APPLET: Number Formats |
Numbers as Polygons
|
Some numbers arise as the number of counters in a layer of regular polygons, either arising from a vertex or centred around a central point.
Applet: Polygonal Numbers |
Cornered and Central Polygonal numbers with 6 layers (above)
and with rays added (below) |
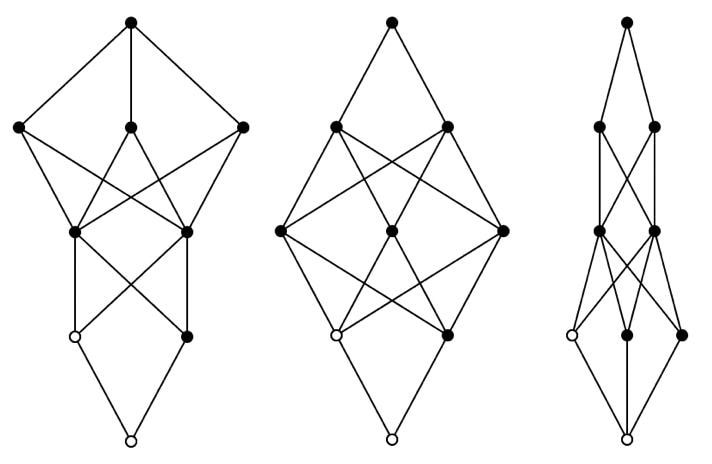
Divisor Lattices and Thread Counts
The lattice of divisors of a number is an amalgam of all the factor trees:
two divisors of N re joined by an edge if and only if the larger divided by the smaller is a prime.
The divisors fall naturally into layers, and the whole has an important structure.
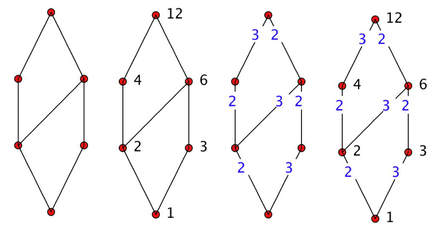
The lcm and gcd (hcf) of two divisors can be found in the lattice. Indeed lattices are an abstraction of the property the each pair of divisors have an lcm and a gcd (hcf).
two divisors of N re joined by an edge if and only if the larger divided by the smaller is a prime.
The divisors fall naturally into layers, and the whole has an important structure.
The lcm and gcd (hcf) of two divisors can be found in the lattice. Indeed lattices are an abstraction of the property the each pair of divisors have an lcm and a gcd (hcf).
the Applet: Divisor Lattices provides the divisor lattice for. number, the various ways in which a thread count gives that number of threads, and a bipartite graph with the same number of edges.